TD 学習によるグリッドワールドのデモ
探索イプシロン: 0.15
セルの報酬変更: (セルを選択してから下のスライダーを左右に動かす)
ゴールに到達するまでの行動数 小さいほど良い:
### セットアップ
このページ (*動的プログラミン法のコピペです*) は 強化学習の文献では 「おもちゃモデル」 としてしばしば使用される **グリッドワールド** という おもちゃの仮想環境です。
ここでは以下のような仮定が置かれます:
- **状態空間** グリッドワールド には 10x10=100 の状態があります。開始状態は左上のセルです。 灰色のセルは壁です。壁を突き抜けて移動することはできません。
- **行為** エージェントは 最大 4 つの行為 を選択することができます。上例では エージェントは最大 4 つの行為から一つの行為を選択して移動することができます。
- **環境ダイナミクス** グリッドワールド は 決定論的です 各状態と行動が与えられるごとに,同じ新しい状態になります。
- **報酬** エージェントは 中央のマス (R 1.0を示すマス) にいるときに +1 の報酬を受け取ります。 いくつかの状態では -1 の報酬を受け取ります(R -1.0 と表示)。 報酬が +1.0 の状態が ゴール状態です。ゴールするとエージェントをスタート状態に戻してリセットします。
この例は 決定論的有限マルコフ決定過程 (MDP) です。
エージェントの目標は常に 将来の割引された報酬 を最大化する エージェントの方策 (矢印で示されている)を見つけることです。
私のお気に入りの部分は 価値反復を収束させ、 セルの報酬を変更して、方策が調整されるのを見ることです。
**インターフェース** セルの色(最初はすべて白)は 現在の方策で その状態の 価値(割引報酬)の現在の推定値を示しています。
任意のセルを選択して **セルの報酬変更** スライダーを使って報酬を変更することができます。
### TD 学習 (Temporal Difference Learning)
TD 法 (有限状態マルコフ決定過程 MDP)は **リチャード サットン Richard Sutton のオンライン教科書** の [第6章](http://webdocs.cs.ualberta.ca/~sutton/book/ebook/node60.html)
に解説があります。
本 REINFORCEjs では 第 7, 9, 8 章 にある数多くの ベルとホイッスル を実装しています。7 章は 適格性トレース (eligibility traces), 8 章は,プランニング, 9 章は関数近似,一般ディープ Q 学習 が記載されています。
重要な概念としては,行動価値関数の推定が挙げられます。
行動価値関数とは,エージェントが受け取る 割引済み期待報酬です。
これは 行動 \\(a\\) を状態 \\(s\\) で行って,任意の方策 \\(\pi(a\\vert s)\\) に従う場合の関数で,次式のとおりです:
$$
Q^\pi (s,a) = E\_\pi \\{ r\_t + \\gamma r\_{t+1} + \\gamma^2 r\_{t+2} + \\ldots \\mid s\_t = s, a\_t = a \\}
$$
上の期待値は,2 つの確率変動するソース,すなわち (1) 環境, (2) エージェントの方策 から成り立っています。
動的プログラミング法とは異なり,TD 学習では,環境と相互作用するエージェントの視点で価値関数を推定します。経験を重ねるたびにその都度方策を更新します。
時刻 t で付番された長い訓練系列 \\(s\_t, a\_t, r\_t, s\_{t+1}, a\_{t+1}, r\_{t+1}, s\_{t+2}, \ldots \\) からエージェントは環境と相互作用します。
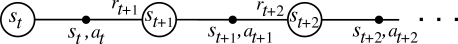 駄菓子菓子,通常の機械学習の設定とは違って,エージェントが採る行動によってその訓練集合が変動します。
知っておくべき重要な概念としては,Q 関数はベルマン方程式を満たしている,ということが挙げられます。
Q 関数とは,一つの行動ノード \\((s\_t, a\_t)\\) から次のノード \\((s\_{t+1}, a\_{t+1})\\) への状態遷移に関係する関数です。以下を見てください:
1. ある状態 \\(s\_t\\) でエージェントは行動 \\(a\_t\\) を採る
2. エージェントは環境から報酬 \\(r\_t\\) を受け取り,状態 \\(s\_{t+1}\\) が更新される
3. エージェントは現在の方策 \\(\pi\\) に従って行動 \\(a\_{t+1}\\) を採る
この行動の元での期待報酬を漸化式を用いて書き表すことができます:
$$
Q(s,a) = \sum\_{s'} \mathcal{P}\_{ss'}^a \left[ \mathcal{R}\_{ss'}^a + \\gamma \sum\_{a'} \pi(s',a') Q(s',a') \right]
$$
ここで,2 つのランダムなソースが足し合わされています。この 2 つとは次の状態とエージェントの現在の方策です。
上式は \\(Q\\) はある数 (すべて 0 とか) で初期化されていて,繰り返し更新されます。
環境のダイナミクス \\(\mathcal{P}\\) を参照することはできません。それでも,エージェントは経験に基づいて環境と相互作用して,未知の分布からサンプルを入手できます。
環境とは違って,方策 \\(\pi\\) は参照可能です。実際には簡単なサンプリングを行う次式で定義される サルサ (SARSA) アルゴリズムが考えられます:
$$
Q(s\_t, a\_t) \leftarrow Q(s\_t, a\_t) + \alpha \left[ \underbrace{r\_t + \gamma Q(s\_{t+1}, a\_{t+1})}\_{target} - \underbrace{Q(s\_t, a\_t)}\_{current} \right]
$$
上式で \\(\alpha\\) は学習率です。カッコ内の量は **TD 誤差 (TD errors)** と呼ばれています。
すなわち,任意の初期値 \\(Q\\) から出発して 方策 \\(\pi\\) を用いて環境と相互作用し,状態と行動と報酬の連鎖 (s, a, r,...) を繰り返すことになります。
この連鎖を訓練データとみなして,その都度確率勾配法によって損失関数,この場合 ベルマンの漸化式 を最小化します。
Q 関数を更新するたびに,方策も貪欲に (greedy) 更新します。サットン本では, **方策反復 policy iteration** が繰り返されます(下図)。
駄菓子菓子,通常の機械学習の設定とは違って,エージェントが採る行動によってその訓練集合が変動します。
知っておくべき重要な概念としては,Q 関数はベルマン方程式を満たしている,ということが挙げられます。
Q 関数とは,一つの行動ノード \\((s\_t, a\_t)\\) から次のノード \\((s\_{t+1}, a\_{t+1})\\) への状態遷移に関係する関数です。以下を見てください:
1. ある状態 \\(s\_t\\) でエージェントは行動 \\(a\_t\\) を採る
2. エージェントは環境から報酬 \\(r\_t\\) を受け取り,状態 \\(s\_{t+1}\\) が更新される
3. エージェントは現在の方策 \\(\pi\\) に従って行動 \\(a\_{t+1}\\) を採る
この行動の元での期待報酬を漸化式を用いて書き表すことができます:
$$
Q(s,a) = \sum\_{s'} \mathcal{P}\_{ss'}^a \left[ \mathcal{R}\_{ss'}^a + \\gamma \sum\_{a'} \pi(s',a') Q(s',a') \right]
$$
ここで,2 つのランダムなソースが足し合わされています。この 2 つとは次の状態とエージェントの現在の方策です。
上式は \\(Q\\) はある数 (すべて 0 とか) で初期化されていて,繰り返し更新されます。
環境のダイナミクス \\(\mathcal{P}\\) を参照することはできません。それでも,エージェントは経験に基づいて環境と相互作用して,未知の分布からサンプルを入手できます。
環境とは違って,方策 \\(\pi\\) は参照可能です。実際には簡単なサンプリングを行う次式で定義される サルサ (SARSA) アルゴリズムが考えられます:
$$
Q(s\_t, a\_t) \leftarrow Q(s\_t, a\_t) + \alpha \left[ \underbrace{r\_t + \gamma Q(s\_{t+1}, a\_{t+1})}\_{target} - \underbrace{Q(s\_t, a\_t)}\_{current} \right]
$$
上式で \\(\alpha\\) は学習率です。カッコ内の量は **TD 誤差 (TD errors)** と呼ばれています。
すなわち,任意の初期値 \\(Q\\) から出発して 方策 \\(\pi\\) を用いて環境と相互作用し,状態と行動と報酬の連鎖 (s, a, r,...) を繰り返すことになります。
この連鎖を訓練データとみなして,その都度確率勾配法によって損失関数,この場合 ベルマンの漸化式 を最小化します。
Q 関数を更新するたびに,方策も貪欲に (greedy) 更新します。サットン本では, **方策反復 policy iteration** が繰り返されます(下図)。
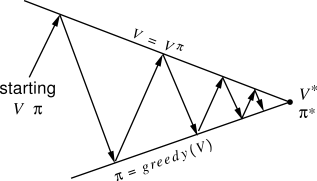 **SARA** は **オン ポリシー** 法と呼ばれます。これは,ある特定の方策から Q 関数を評価するために,オン(ポリシー) と呼ばれるからです。
複数の方策から Q 関数をコントロールするような場合の方が良い場合があります。
これは **Q 学習** と呼ばれ,次式で定義されます。
$$
Q(s\_t, a\_t) \leftarrow Q(s\_t, a\_t) + \alpha \left[ r\_t + \gamma \max\_a Q(s\_{t+1}, a) - Q(s\_t, a\_t) \right]
$$
Q 学習は **オフ ポリシー** と呼ばれます。最適な 行動価値関数 \\(Q^\*\\) と 実際の Q 関数が近似する方策とが一致しないからです。
直感的には,このような更新方法は **楽観的** に見えます。
最適な行動に基づく Q 関数の方針が
なぜなら 現在の行動方針でたまたまサンプリングした行動に基づくのではなく, 状態 \\(s_\{t+1}\\) で取りうる最善の行動の推定値に基づいて Q 関数を更新するからです。
この グリッドワールドのデモでも SARSA よりも Q 学習の更新の方がはるかに速く収束します。
**探索 Exploration**. TD 学習をうまく動作させるために必要な最後の構成要素は,ある程度の **探索** を明示的に確保することです。
もしエージェントが常に現在の方策に意固地に従うのならば,最適化中に局所最小値に陥ることが起きるでしょう。これと同様にして,探索に行き詰まる危険性があります。
ある程度の (ランダムに) 探索を保証する (かつ,すべての収束保証を担保する) ため,一般的で簡単な方法を使います。
これが **イプシロン貪欲 epsilon greedy** な探索と呼ばれる方法です。
つまり、確率 イプシロン \\(\epsilon\\) でエージェントはランダムな行動をとり,残りは現在のポリシーに従います。
このイプシロンの値通常 0.1, 0.2, くらい,訓練中は,非常に小さな値 (例えば 0.05 や 0.01 など) に緩徐 (アニーリング) されます。
### TD の ベルとホイッスル (Bells and Whistles)
(訳注: ベルとホイッスルとは,本質ではないけど魅力的なオマケ的な意味です)
上のデモのオプションを見てみると 'qlearn' か 'sarsa' だけでなく, 割引率 `spec.gamma`, 探索パラメータイプシロン `spec.epsilon`, 学習率 `spec.alpha` があります。他には次のものあります。
**妥当性の痕跡 eligibility traces** 妥当性の痕跡の背後にあるアイデアは,TD 更新 を より局所的なものにせず, 過去の経験の一部を介して 後方に拡散させることです。
言い換えれば,エージェントが以前どこにいたかの (減衰する) 痕跡(トレース) を保持しておくことです。
減衰率は ハイパーパラメータ \\(\lambda\\) で制御します。
Q 値の更新は s,a,r,s,a,r,s,a,s,a,r... チェーンの 1 つのリンクだけでなく,最近の行動履歴に沿って実行します。
これは Q 値がある状態 (s,a) について変化するとき,その直前の他のすべての状態も,再帰的依存性のために影響を受けるという事実から正当化さます。
例えば あるグリッドワールドで 報酬を発見した場合 エージェントは 直前の状態の Q 値 を更新するだけでなく,その状態に至るまでに見てきた状態の Q 値 も更新することになります。
この場合 0 値は トレースを使用しないことを意味します (デフォルト)。
**SARA** は **オン ポリシー** 法と呼ばれます。これは,ある特定の方策から Q 関数を評価するために,オン(ポリシー) と呼ばれるからです。
複数の方策から Q 関数をコントロールするような場合の方が良い場合があります。
これは **Q 学習** と呼ばれ,次式で定義されます。
$$
Q(s\_t, a\_t) \leftarrow Q(s\_t, a\_t) + \alpha \left[ r\_t + \gamma \max\_a Q(s\_{t+1}, a) - Q(s\_t, a\_t) \right]
$$
Q 学習は **オフ ポリシー** と呼ばれます。最適な 行動価値関数 \\(Q^\*\\) と 実際の Q 関数が近似する方策とが一致しないからです。
直感的には,このような更新方法は **楽観的** に見えます。
最適な行動に基づく Q 関数の方針が
なぜなら 現在の行動方針でたまたまサンプリングした行動に基づくのではなく, 状態 \\(s_\{t+1}\\) で取りうる最善の行動の推定値に基づいて Q 関数を更新するからです。
この グリッドワールドのデモでも SARSA よりも Q 学習の更新の方がはるかに速く収束します。
**探索 Exploration**. TD 学習をうまく動作させるために必要な最後の構成要素は,ある程度の **探索** を明示的に確保することです。
もしエージェントが常に現在の方策に意固地に従うのならば,最適化中に局所最小値に陥ることが起きるでしょう。これと同様にして,探索に行き詰まる危険性があります。
ある程度の (ランダムに) 探索を保証する (かつ,すべての収束保証を担保する) ため,一般的で簡単な方法を使います。
これが **イプシロン貪欲 epsilon greedy** な探索と呼ばれる方法です。
つまり、確率 イプシロン \\(\epsilon\\) でエージェントはランダムな行動をとり,残りは現在のポリシーに従います。
このイプシロンの値通常 0.1, 0.2, くらい,訓練中は,非常に小さな値 (例えば 0.05 や 0.01 など) に緩徐 (アニーリング) されます。
### TD の ベルとホイッスル (Bells and Whistles)
(訳注: ベルとホイッスルとは,本質ではないけど魅力的なオマケ的な意味です)
上のデモのオプションを見てみると 'qlearn' か 'sarsa' だけでなく, 割引率 `spec.gamma`, 探索パラメータイプシロン `spec.epsilon`, 学習率 `spec.alpha` があります。他には次のものあります。
**妥当性の痕跡 eligibility traces** 妥当性の痕跡の背後にあるアイデアは,TD 更新 を より局所的なものにせず, 過去の経験の一部を介して 後方に拡散させることです。
言い換えれば,エージェントが以前どこにいたかの (減衰する) 痕跡(トレース) を保持しておくことです。
減衰率は ハイパーパラメータ \\(\lambda\\) で制御します。
Q 値の更新は s,a,r,s,a,r,s,a,s,a,r... チェーンの 1 つのリンクだけでなく,最近の行動履歴に沿って実行します。
これは Q 値がある状態 (s,a) について変化するとき,その直前の他のすべての状態も,再帰的依存性のために影響を受けるという事実から正当化さます。
例えば あるグリッドワールドで 報酬を発見した場合 エージェントは 直前の状態の Q 値 を更新するだけでなく,その状態に至るまでに見てきた状態の Q 値 も更新することになります。
この場合 0 値は トレースを使用しないことを意味します (デフォルト)。
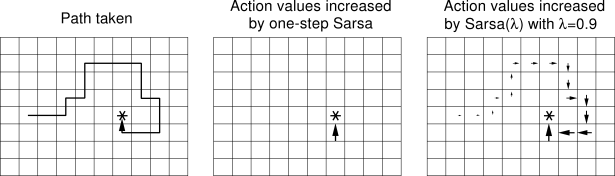
図はサットン本より,妥当性の痕跡の基本概念を示している
さらに `spec.replacement_traces` (デフォルトはtrue) で制御可能なオプションがあります。
このオプションは,痕跡を置き換えるか,痕跡を蓄積するかのどちらかを指定します。
このオプションの設定の違いは,同じ状態が複数回訪れたときに痕跡ががどのように蓄積されるを決めます。
毎回更新するか,定められた最大値にリセットするかです。
繰り返しになりますが サットン本の素晴らしい図は 1 つの状態が繰り返し訪れたときのトレースの強さを示していてポイントをうまく伝えています。
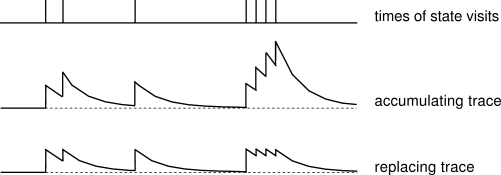
**プランニング Planning** TD 法は,環境モデルを推定する必要がありません。
このため,デフォルトでは モデルフリーと呼ばれています。
つまり,エージェントは,遷移確率や環境がエージェントに与える報酬を知る必要はありません。
エージェントは,これらの値のサンプルを観察して,行動値関数 Q の中にそれらの十分な統計量を抽出することを行います。
プランニングにおける基本的な考え方は,環境がどのように機能するかのモデルを明示的に維持することです。
すなわちエージェントは,観測データから訓練されるという意味で,どのような状態や行動がどのような他の状態につながり,どのように報酬が割り当てられるかを経験するということです。
言い換えればエージェントは,学習データの痕跡 \\(s\_t, a\_t, r\_t, s\_{t+1}, a\_{t+1}, r\_{t+1}, s\_{t+2}, \ldots\\) に基づいて,環境モデルを追従します。
$$
Model(s,a) \leftarrow s', r
$$
例えば このグリッドワールドのデモでは,簡単なルックアップ表で \\(s,a\\) のすべての対を探しています。
このグリッドワールドが決定論的であるという事実は,ルックアップ表がすべて固定された不変の値であり,観察して覚えておくのが簡単だからです。
このモデルは、体験を仮想的に実現させたものです。これは以下のような *フェイク* 体験に基づいて更新を行ったりするのに役立ちます。
1. 実世界の行動 \\(a\\) を実行する
2. 環境から 新しい状態 \\(s'\\) と報酬 \\(r\\) とを受け取る
3. TD 更新 (Q 学習による更新など) を実施する
4. 環境モデルを更新する \\(\text{Model}(s,a) \leftarrow s', r\\)
5. これを **N回** 繰り返す。いくつかの \\(s,a\\) をサンプルし,モデルを用いて \\(s′,r\\) を予測し,この仮想体験について Q学習 の更新を実行する
環境モデルを使用して,ステップごとに多くの値関数の更新を行っていることに注目してください。
実際には (このデモでも) これはかなりの量の収束を助けることができます。
`spec.planN` (0 = 計画なし)では,反復あたりの計画ステップ数 (偽の経験値更新)を制御することができます。
直感的には,これがこれほどうまく機能する理由は,エージェントが高報酬の状態を発見したときに,環境モデルがその状態に到達する方法を知っているからです。
このデモでは,最初に高報酬状態が発見されたときに,矢印が「魔法のように」正しい方向を指し始めます。
**拘束更新スケジュールのための優先キュー (Priority queue for faster update schedule)**. REINFORCEjs によって実装されている追加のホイッスルがあります。
ランダムな **N個の状態** をサンプリングして更新を実行するのではなく,最も更新を必要とする状態を追跡し,優先的にキュー(待ち行列)から取り出します。
直感的には,各更新中の TD 誤差は,その更新がどれだけ驚くべきものであるかを教えてくれます。
ある状態 \\(s\\) の Q 値を大きな TD 誤差で更新したとします。
このとき \\(s\\) につながると予測されるすべての状態についてモデルを照会し,TD 誤差の大きさを優先して優先度キューに配置することができます。
このようにして,どこか遠くにあって更新がほとんど必要ない状態をサンプリングして時間を無駄にしないようにしています。
このグリッドワールドのデモでは,エージェントが最初に報酬状態を発見したときに,大きな正の TD 誤差が発生し,すぐに報酬状態に至るまでのすべての状態が優先度の高い優先度キューに配置されます。
それゆえ,Q 値は Q 関数全体を通して可能な限り最速の方法で拡散し,同期します。
これはデフォルトでオンになっています(設定はありません)。
**スムーズ Q 関数更新 (Smooth Q function updates)**. 最後の REINFORCEjs の設定は `spec.smooth_policy_update` と `spec.beta` です。
この 2 つは非標準です。
より良い可視化のために追加しました。
これら設定では,確率的な方策を使っています。
ですが,最大値を取る行動にゆっくりと収束するようにスムーズに方策を更新しています。
これにより,方策の矢印がより良く,より滑らかに可視化されます。
### TD 法で用いられる REINFORCEjs の API
動的プログラミング DP 法と同様,REINFORCEjs の TD 法を使う場合には,環境用オブジェクト `env` を定義します。
`env` は TD エージェントに必要なメソッドが用意されています.
- `env.getNumStates()` 総状態数を返す
- `env.getMaxNumActions()` 任意の状態での行動の最大値 (整数) を返す
- `env.allowedActions(s)` 引数 `s` (整数) をとり,可能な行動のリストを返す。戻り値は 0 から `maxNumActions` までの整数
このデモのソースコードの GridWorld 環境を参照してください。
クラス `TDAgent` は有限の マルコフ決定過程 MDP (離散的な有限状態と行動) を想定しています。
単純な `action = agent.act(state)` と `agent.learn(reward)` というインタフェースを介して動作します。
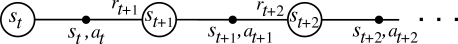


図はサットン本より,妥当性の痕跡の基本概念を示している

// 環境を作成
env = new Gridworld();
// エージェントを作成
var spec = { alpha: 0.01 } // このページ上部の全オプションを参照してください
agent = new RL.TDAgent(env, spec);
setInterval(function(){ // 学習ループ開始
var action = agent.act(s); // s は整数,行動 (action) も整数
// ある環境で行動を一度実行し,報酬を得る
agent.learn(reward); // エージェントが Q,方策,モデルなどを更新
}, 0);