パックマンワールド: ディープ Q 学習
探索イプシロン: 0.15
Experience write pointer:
現在の TD 誤差:
平均報酬 (高いほど良い)
### セットアップ Setup
このデモは,**パックマンワールド** の修正版です
- **状態空間** は拡張され,連続値になっています。
エージェントは自分の位置 (x,y) , 速度 (vx, vy) を観察します。緑色のターゲットと赤のターゲットの場所,全部で 8 つです。
- エージェントは 4 つの行動を撮ることができます。
- パックマンワールドの **ダイナミクス** では エージェントの位置を変更するための速度を統合します。
緑のターゲットは,時々ランダムな場所に移動します。
赤のターゲットは常にエージェントにゆっくりと追従します。
- **報酬 reward** は緑のターゲットまでの距離です。緑との距離は低いほど良いと評価されます。
一方,エージェントが赤いターゲットの近く(ディスクの内側)にいる場合,エージェントと赤いターゲットまでの距離に比例して負の報酬を得ます。
エージェントにとっての最適な戦略は,常に緑のターゲット (これは通常のパックマンワールドです)に向かって行くことです。
ですが,赤のターゲットの効果範囲を避けることが必要です。
これにより,エージェントは赤ターゲットを避けることを学ばなければならないので,ゲームをより面白くしています。
また、赤いターゲットがエージェントを追い詰めるのを見るのも楽しいです。
この場合に最適なのは,追い詰められたときに多くの報酬を支払うより,一時的に素早くズームして離れていくための代償を支払うことです。
**インターフェイス**: エージェントが経験した現在の報酬は 色 (緑=高,赤=低) で示されています。エージェントが取った行動 (中程度の大きさの円が動き回っている) が矢印で示されています。
### 深層 Q 学習 (Deep Q Learning)
TD 学習 (Q-学習) を連続状態空間に拡張してみます。
先のデモでは,Q 学習 関数 \\Q(s,a)\\) をルックアップテーブルとして推定しました。
ここで \\(Q(s,a) = f\_{\theta}(s,a)\\), をモデル化するために関数近似器を使用しようとしていますが、\\(\theta\\) はいくつかのパラメータ (例えば ネットワーク内のニューロンの重みやバイアス)です。
しかし,これから見るように,他のすべてのことはまったく同じです。
このアプローチで印象的な結果を示した最初の論文は,2013 年の NIPSワークショップ での [Playing Atari with Deep Reinforcement Learning](http://arxiv.org/abs/1312.5602) です。
さらに最近では Nature 論文 [Human-level control through deep reinforcement learning](http://www.nature.com/nature/journal/v518/n7540/full/nature14236.html) です。
両方とも Mnih らによるものでした。これをすべてJSで動作させるのは難しい。
Q 学習では,学習データは \\(s\_t, a\_t, r\_t, s\_{t+1}, a\_{t+1}, r\_{t+1}, s\_{t+2}, \ldots \\) の単一連鎖です。
状態 \\(s\\) と報酬 \\(r\\) は環境ダイナミクスからのサンプルです。
行動 \\(a\\) はエージェントのポリシー \\(a\_t \sim \pi(a \mid s\_t)\\) からのサンプルであることを想起してください。
Q 学習におけるエージェントの方策は,現在最も高い値を持つと推定される行動
(\\( \pi(a \mid s) = \arg\max\_a Q(s,a) \\)) を実行するか,または 確率 \\(\epsilon\\) でランダムな行動をとって何らかの探索を確実に行うことです。
そして、各時間ステップにおける Q 学習 の更新は、以下のような形式です:
$$
Q(s\_t, a\_t) \leftarrow Q(s\_t, a\_t) + \alpha \left[ r\_t + \gamma \max\_a Q(s\_{t+1}, a) - Q(s\_t, a\_t) \right]
$$
上式は,学習率 \\(\alpha\\) で確率的勾配降下法を用いて更新される,時刻 \\(t\)) での次式の損失関数が用いられます:
$$
L\_t = (r\_t + \gamma \max\_a Q(s\_{t+1}, a) - Q(s\_t, a\_t))^2
$$
ここで \\(y = r\_t + \gamma \max\_a Q(s\_{t+1}, a)\\) は,スカラ値です。この値で誤差逆伝播法により学習します。
損失関数は標準的な L2ノルム回帰の形をしていることに注意してください。
\\(\theta\\) のパラメータベクトルを 計算された \\(Q(s,a)\\) の値が、あるべき姿に少しだけ近づくように,(ベルマン方程式を満たすように) 調整されます。
これは,報酬が適切に拡散されるべきであるという制約を,環境ダイナミクスとエージェントの方策を介して,期待して,後方へ伝播するものです。
In other words, Deep Q Learning is a 1-dimensional regression problem with a vanilla neural network, solved with vanilla stochastic gradient descent, except our training data is not fixed but generated by interacting with the environment.
言い換えれば,ディープ Q 学習は 素のニューラルネットワークを用いた 1次元回帰問題です。
学習データが固定ではなく,環境との相互作用によって生成されることを除いては、素の確率的勾配降下法で解くことができます。
### ベルとホイッスル (Bells and Whistles)
実践的な問題で関数近似をトラックテーブルにした Q 学習をするためのいくつかのベルとホイッスルがあります。
**Modeling Q(s,a)**. 前述したように Q 関数 \\(Q(s,a) = f\_{\theta}(s,a)\\) をモデル化するために関数近似器を使用しています。
取るべき自然なアプローチは,おそらく状態ベクトル \\(s\\) と行動ベクトル \\(a\\) 例えば ワンホットベクトルでエンコードされた入力を受け取り,
\\(Q(s,a)\\) を与える単一の数値を出力するニューラルネットワークを作る持つことです。
しかし,この方法では,エージェントの方策は Q 値を最大化する行動をとること,
すなわち \\( \pi(a \mid s) = \arg\max\_a Q(s,a) \\) です。
このため,実用的な問題が発生します。
この素朴な方法アプローチでは,エージェントが行動を生成しようとすると,すべての行動を反復処理し,それぞれの行動について Q 値を評価し,
最も高い Q を与えた行動をとらなければなりません。
それよりより良いアイデアは,状態 \\(s\\) だけを取り,複数の出力を生成するニューラルネットワークとして
値 \\(Q(s,a)\\) を予測するかわりに,複数の出力を生成することです。
これらの値は,それぞれが与えられた状態でその行動を取る際の Q 値として解釈されます。
このようにして,どのようなアクションを取るかを決定することは,ネットワークの一回のフォワードパスを実行して 最大値を与える行動を見つけることに縮約されます。
図を見ていただければ理解していただけると思います。
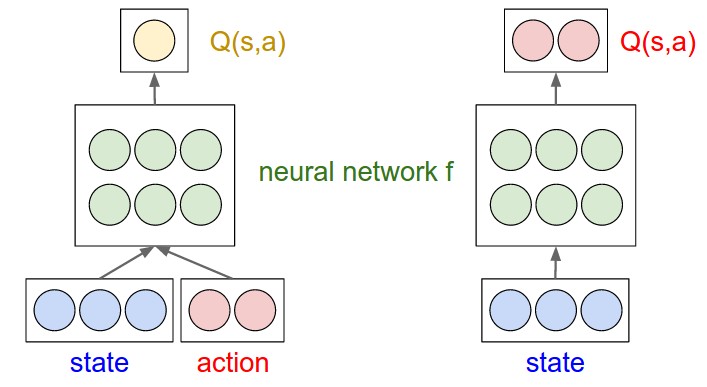
3 次元の状態空間(青)と 2 つの行動(赤)の単純な例。緑のノードはニューラルネットワーク f のニューロン。 左: 最大値を与える行動を見つけるために複数回の前向きパスを取る素朴ななアプローチ。 右: より効率的なアプローチ。 Q(s,a) の計算がネットワーク内のニューロン間で効果的に共有される。 与えられた状態で取るべき最良の行動を見つけるためには 1 回の前向きパスのみが必要。
このように定式化すると、更新アルゴリズムは次のようになります。
1. 環境中で \\(s\t, a\_t, r\_t, s\_{t+1}\\) の遷移を経験する
2. 前向きパス \\(s\_{t+1}\\) で (固定の)目標 \\(y = r\_t + \gamma \max\_a f\_{\theta}(s\_{t+1})\\) を評価する。
3. 前向き \\(f\_{\theta}(s\_t)\\) で 次元 \\(a\_t\\) に L2 損失を適用する。 L2 損失のため 勾配は単純な形をしており,予測値は単純に \\(y\\) から減算される。
4. 勾配を逆伝播し,パラメータを更新する
**Experience Replay Memory**. Mnih らの論文の重要な貢献は,経験のリプレイ記憶を示唆することでした。
これは 脳、特に海馬の記憶痕跡を大脳皮質と同期させる方法から着想を得たものです。
これは,更新してから経験を捨てるのではなく,経験を残しておいて,効果的に経験の訓練セットを作り上げるということです。
そうすると,その時に入ってきた経験を元に学習するのではなく,リプレイメモリからランダムに経験をサンプリングして,それぞれのサンプルを更新してきます。
繰り返しになりますが,これは,通常の機械学習のセットアップでデータセット上で 確率的勾配降下法 (SGD) を使ってニューラルネットを学習する場合と全く同じです.
違いはデータセットがエージェントの相互作用の結果であることだけです。
この機能は,観察された状態,行動,報酬の順序の相関関係を除去する効果があり,段階的なドリフトと忘却を減少させます。
アルゴリズムは以下の通り:
1. ある環境で \\(s\_t, a\_t, r\_t, s\_{t+1}\\) を経験し,訓練データセットに加える。もし閾値よりも大きければ,過去の経験を置き換える
2. **N** このサンプルを \\(\mathcal{D}\\) から取得し,Q 関数を更新する
**Clamping TD Error**. もう一つの興味深い特徴は TD 誤差勾配を一定の最大値でクランプすることです。
つまり TD 誤差 \\(r\_t + \gamma \max\_a Q(s\_{t+1}, a) - Q(s\_t, a\_t)\\) が大きければ その最大値でクランプ(その最大値にしてしまう)する。
これにより,外れ値に対してより頑健な学習が可能になり Huber 損失を利用するという解釈もできます。
**Periodic Target Q Value Updates**. Mnih ら で提案された最後の修正もまた,更新とすぐに実行される動作の間の相関を減らすことを目的としています。
そのアイデアは Q ネットワーク を時々凍結させ,凍結されたコピーされたネットワーク \\(\hat{Q}\\) にして,ターゲットのみを計算するために使用することです。
このターゲットネットワークは,時々,実際の現在のQネットワークに更新されます。
つまり,ターゲットの計算にはターゲットネットワーク \\(r\_t + \gamma \max\_a \hat{Q}(s\_{t+1},a)\\) を使用し,\\(Q(s\_t, a\_t)\\) の部分の評価には Q を使用します。
実装では \\(\hat{Q} \leftarrow Q\\) を同期させるためのコードを 1 行追加する必要があります。
このアイデアで遊んでみましたが,少なくともこの単純なおもちゃの例では,実質的な利益を与えるとは思えなかったので,簡潔にするために現在の実装では REINFORCEjs から外してあります。
### DQN に用いられる REINFORCEjs API
If you'd like to use REINFORCEjs DQN in your application, define an `env` object that has the following methods:
- `env.getNumStates()` returns an integer for the dimensionality of the state feature space
- `env.getMaxNumActions()` returns an integer with the number of actions the agent can use
This seems kind of silly and the name `getNumStates` is a bit of a misnomer because it refers to the size of the state feature vector, not the raw number of unique states, but I chose this interface so that it is consistent with the tabular TD code and DP method. Similar to the tabular TD agent, the IO with the agent has an extremely simple interface:

3 次元の状態空間(青)と 2 つの行動(赤)の単純な例。緑のノードはニューラルネットワーク f のニューロン。 左: 最大値を与える行動を見つけるために複数回の前向きパスを取る素朴ななアプローチ。 右: より効率的なアプローチ。 Q(s,a) の計算がネットワーク内のニューロン間で効果的に共有される。 与えられた状態で取るべき最良の行動を見つけるためには 1 回の前向きパスのみが必要。
// create environment
var env = {};
env.getNumStates = function() { return 8; }
env.getMaxNumActions = function() { return 4; }
// create the agent, yay!
var spec = { alpha: 0.01 } // see full options on top of this page
agent = new RL.DQNAgent(env, spec);
setInterval(function(){ // start the learning loop
var action = agent.act(s); // s is an array of length 8
// execute action in environment and get the reward
agent.learn(reward); // the agent improves its Q,policy,model, etc. reward is a float
}, 0);