ディープラーニングの心理学的解釈 (心理学特講IIIA)

Shin Aasakawa, all rights reserved.
Date: 22/May/2020
Appache 2.0 license

本日のキーワード

  • 訓練データ，テストデータ，検証データ
  • ニューラルネットワーク neural networks
  • パーセプトロン perceptron
  • 畳み込みニューラルネットワーク convolutional neural netoworks

  • レティノトピー retinotopy, トノトピー tonotopy, ソマトピー somatopy,

  • 誤差逆伝播法 error back propagation

  • 損失関数 loss functions, 誤差関数 error functions, 目的関数 objective functions, 目標関数 target functions
  • 勾配降下法 gradient descent methods
  • ソフトマックス関数 softmax function
  • 交差エントロピー cross entropy
  • 確率的勾配降下法 stochastic gradient descent methods

色を薄くしてあるのは，ここまで進まないだろうという予想しているからです。

クイズの答え:

  • ANN: 人工ニューラルネットワーク Artificial Neural Networks
  • BNN: 生物学的ニューラルネットワーク Biological Neural Networks
  • CNN: 畳み込みニューラルネットワーク Convolutional Neural Networks
  • DNN: 深層ニューラルネットワーク Deep Neural Networks

小ネタ

  • ANN, BNN, CNN, DNN は冗談です。 この分野以外では，もちろん ANN は オールナイトニッポンであったり，BNN はブルームバーグニュースネットワークだったり， CNN はケーブルニュースネットワークだったりします。 DNN は市民権を得てきた感があるので ディープニューラルネットワークで良いでしょう

  • colab に自分のためののコメントを書くために markdown の書式を覚えておいた方が良いです。(補講で少し取り上げました)

  • 最先端の話をしています。画像処理が人間を超える性能を示すようになったから，最近の AI ブームがあります。 これは，第二回の授業でも取り上げました。だからこそ，この授業があります。干からびた化石のような知識を教えるつもりはありません。

  • ジェフェリー・ヒントンのマクセル賞受賞記念講演(2016)

  • 次元圧縮 t-SNE
  • データサイエンス小史
  • 数式の読み方
  • 苦い教訓

実習


from Difference between AlexNet, VGGNet, ResNet, and Inception

CNN の特徴

  • 次の 7 つを上げることができます 。

  • 非線形活性化関数 (nonlinear activation functions)

  • 畳込み演算 (convolutional operation)
  • プーリング処理 (pooling)
  • データ拡張 (data augmentation)
  • バッチ正規化 (batch normalization)
  • ショートカット(shortcut)
  • GPU の使用

上記 7 つの特徴を説明するのは専門的になりすぎるので省略します。一つだけ説明するとすれば最後の GPU とは高解像度でしかも処理速度を必要とするパソコンゲームで用いられるグラフィックボードのことです。 詳細な画像を高速に画面に表示する必要から開発されたグラフィックボードですが，大規模なニュールネットワークの計算でも用いられる数学が同じです。 そのため，ゲーム用に開発されたグラフィックボードがニューラルネットワークにも用いられるようになりました。

ディープラーニングの特徴

from Democratize AI slides

  • データハングリー data hungry
  • 計算資源ハングリー resource hungry
  • 理論欠如 theory lagging

  • 不透明 opacity

  • ニューラルネットワークは素人の統計学である, Anderson et. al (1993)

... But Neural networks are not alchemy.

1. 生理学


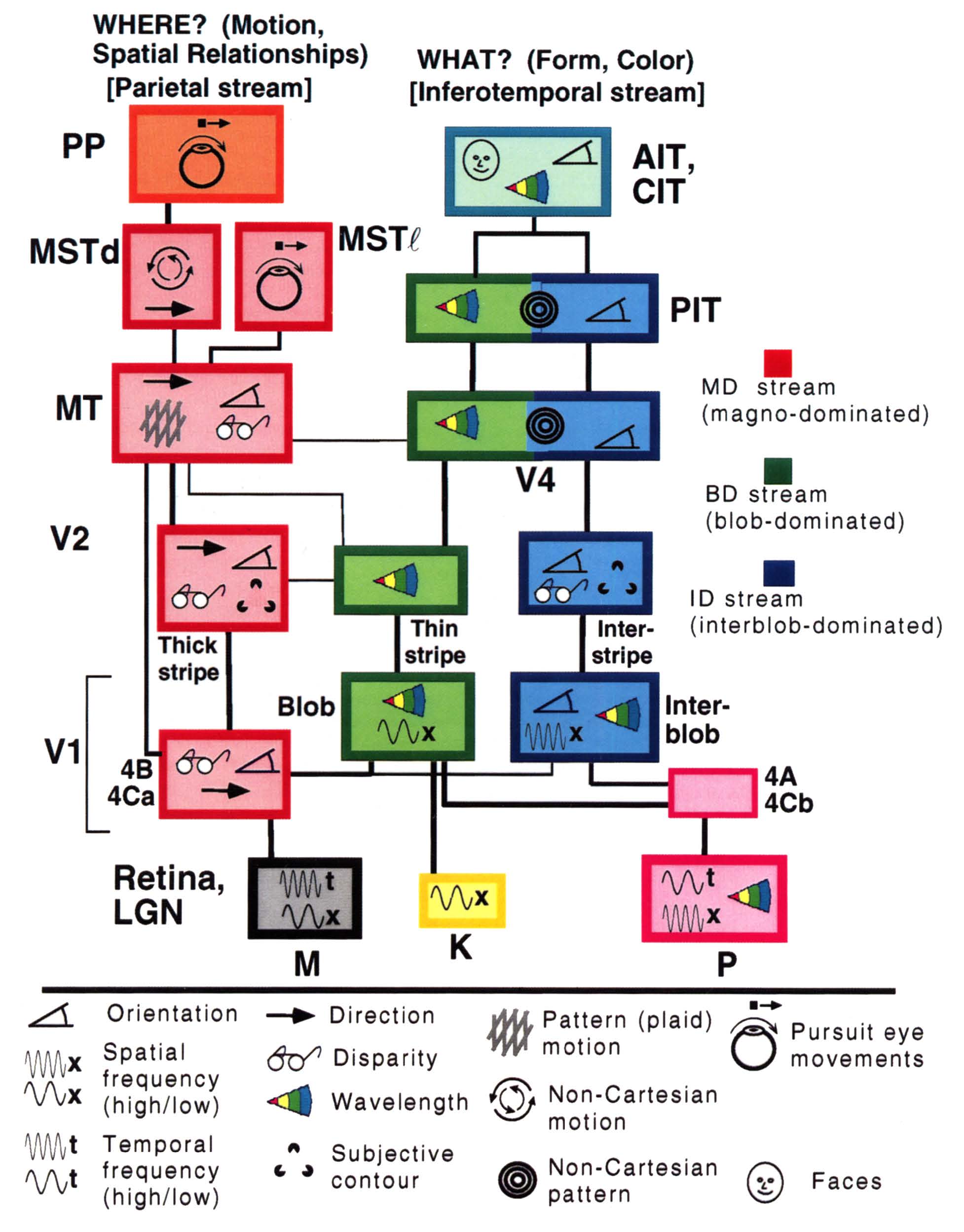Van Essen & Gallant (1994)


Left: Thorpe et al.(2001), Right: Felleman & Van Essen (1992)


source: https://en.wikipedia.org/wiki/Retinotopy

ヒューベルとウィーゼル Hubel and Wiesel (1969)


source: https://youtu.be/4nwpU7GFYe8

  • トポグラフックマッピング topographic mappings (地形図): 網膜や皮膚などの体制感覚，筋肉系のような効果器系を、中枢神経系の 1 つ以上の構造物に整然と投影した地図。 地形図は、すべての感覚系と多くの運動系で観察される。
  • トノトピー tonotopy（ギリシャ語のtono=周波数、topos=場所）とは、異なる周波数の音が脳内で処理される場所の空間的配置のこと。 周波数が近い音は、脳内の場所的に隣接する領域で表現される。トノトピック地図とも呼ばれる
  • ソマトピー somatopy: 中枢神経系上の特定の点へ身体領域の照射，投影のこと。 身体領域は 第一次体性感覚皮質 (後腹回) に投影される。 典型的には 特定の身体部位と そのそれぞれの位置を ホムンクルス homunclus (小人) 上に配置する 感覚ホムンクルスとして表現される。 細かく制御されている部位 (指，舌) は体性感覚野の面積が大きい。一方 粗く制御されている部位 (体幹) は面積が小さい。内臓のような領域は体性感覚野の位置を持たない。
  • レティノトピー retinotopy: 網膜からの視覚入力を神経細胞 にマッピングすること。哺乳類の脳に多く見られる。この地図の大きさ、数、空間的配置は種間で異なる。 視野の隣接する点 が 同じ領域 の 隣接する 領域で 表現される とは限らないという意味で、複雑な地図となる。 例えば 第 2 次視覚野 (V2) での視覚地図は 視野の上半分に応答する網膜の部分が 視野の下半分に応答する部分から分離されて表現されている。第３次視覚野 (V3) や 第4次視覚野 (V4) では下位の視覚野に比べて より複雑な表現がなされている

ブレイクモア と クーパー Blackmore and Cooper (1970)


source: https://youtu.be/QzkMo45pcUo


source: https://youtu.be/RSNofraG8ZE

一アルゴリズム仮説 One algorithm hypothesis

Sur (1988) より


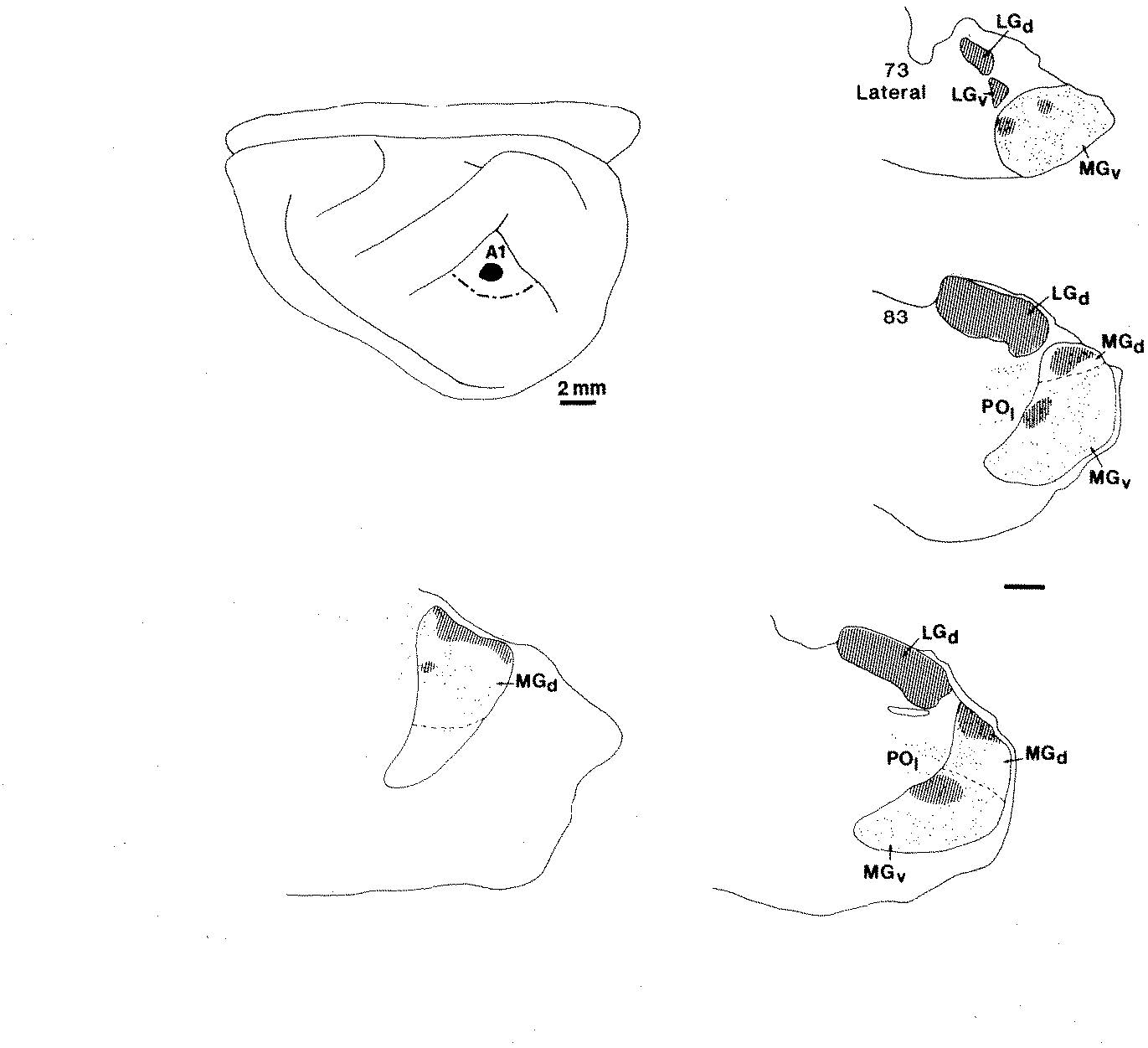
聴覚視床への実験的に誘導された網膜投影（ハッチングされた領域）および聴覚視床と聴覚皮質の接続。 手術した半球とは反対側の眼は、生き残っている背側LGN（LGd）と腹側LGN（LGv）、およびMGNの背側と腹側の区画内のパッチ（それぞれMGdとMG）に投影する。 視床の傍矢状切片を番号付きで示す。 視床の傍矢状切片の 同じ動物に、一次聴覚野（Al）にHRPを注入した場合（注入部位は左上に示す）、細胞が充填される。 ドットで示されている）MG "MGdでは逆行性に、MGvでは後遺症複合体の側方分裂（P01）が行われている。MGdとMGvの多くの細胞が網膜突起帯を覆っている。

  • Metin and Frost (1989) Visual responses of neurons in somatosensory cortex of hamsters with experimentally induced retinal projections to somatosensory thalamus
  • Roe et al. (1992) Visual Projections Routed to the Auditory Pathway in Ferrets: Receptive Fields of Visual Neurons in Primary Auditory Cortex

2. 心理学

セルフリッジ Selfridge のパンデモニウム pandemonium モデル


セルフリッジ (1958) ``Mechanisation of Thought Processes'' より


セルフリッジ (1958) ``Mechanisation of Thought Processes'' より



セルフリッジ (1958) ``Mechanisation of Thought Processes'' より

生理学，視覚心理学との対応

  • Julesz
  • Julesz (1981) Textons, the elements of texture perception, and their interactions, Nature


Julesz (1981) Fig. 2 より

  • Marr
    • Computational approach: Vision (1908)
  • Poggio
    • Poggio, Torre, and Koch (1985) Computational vision and regularization theory

心理学モデル Psycholosophical consideration

  • Epistemology 思念的，観念的
  • Empirical Episitemology 実証的 = psychology

  • Constructive epipstemology 構成論的 = computer vision, neural networks

  • Marr

    • Computational approach: Vision (1908)
  • Poggio
    • Poggio, Torre, and Koch (1985) Computational vision and regularization theory

生理学との対応 (Hubel and Wiesel のネコとサル, Blackmore のネコ, ヴァンエッセン)

  • 層間の結合の仕方, アーキテクチャ
  • forward/backward 役割，機能，実現方法
  • 側抑制 lateral inhibition (これについては多層化して回避できる可能性あり)

  • shape from X は正しかったのか？ ただし発達心理学におけるシェイプバアスは言語発達において重要な意味を持つはず。だからと言って乳幼児はそのように強制(脅迫？)，矯正されて育つわけではないだろう。

    • Ritter (2017) Cognitive Psychology for Deep Neural Networks: A Shape Bias Case Study
    • Landau, Smith, Jones (1992) Syntactic Context and the Shape Bias in Childrens and Adults Lexical Learning

    • Yamins (2016) Using goal-driven deep learning models to understand sensory cortex

    • Julez のアプローチは視覚研究者 Haar, SIFT, DoG などのアルゴリズム開発者と対応

    • Poggio (1985) Computational Vision and Regularization Theory

Marr and Poggio (1976)

中枢神経系は 4 つのほぼ独立したレベルの記述で理解される必要がある。 1. 計算の性質が表現されるレベル、 2. 計算を実装するアルゴリズムが特徴づけられるレベル、 3. アルゴリズムが特定のメカニズムにコミットされるレベル、 4. メカニズムがハードウェアで実現されるレベル

である。 一般的に、計算の性質は解決すべき問題によって決定され、使用されるメカニズムは利用可能なハードウェアに依存し、選択される特定のアルゴリズムは問題と利用可能なメカニズムに依存する。

のちに 3 つにまとめられ，それが有名になりました。ですが，出始めは 4 つでした。他の授業では Marr の 3 水準と呼ばれるかも知れません。 その有名になった Marr の 3 水準とは 1. 計算論 2. アルゴリズム 3. 実装 にあたります。脳を理解する上で，3 つを区別して考えましょうというスローガンです。

現代的ニューラルネットワークモデルと生理学との対応



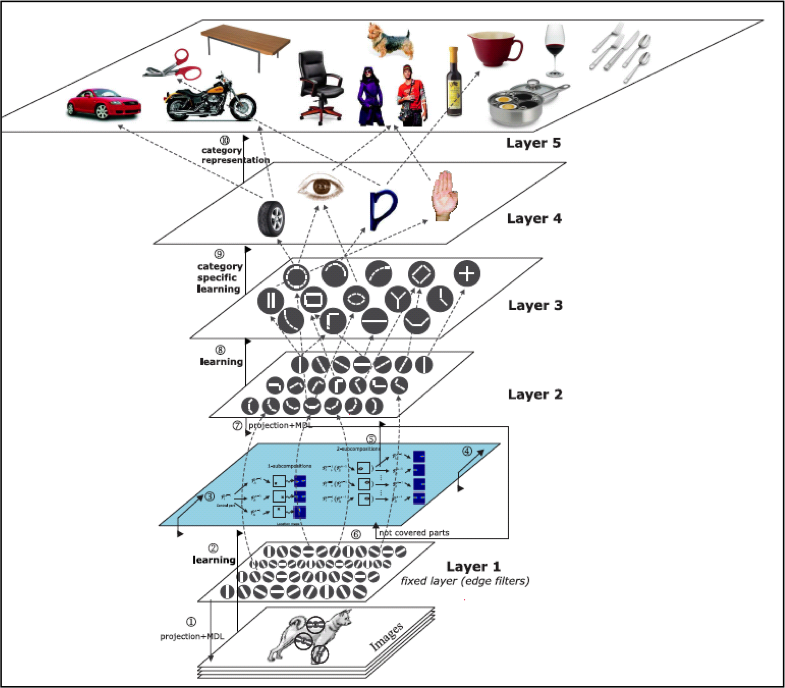
Zeiller 2012 より

Zeiler et. al. (2010) Fig. 7, and 8


目標駆動型モデリングの構成要素。 内側の円は、与えられた数のレイヤーのモデルを含む完全なモデルクラスの部分空間を表す。 目標駆動モデルは、特に最適なモデルを発見するために、モデル・クラス内の軌道（実線）に沿ってシステムを駆動する学習アルゴリズム（黒の点線矢印）を使用して構築される。 各ゴールは、そのゴールを解くのに特に適したパラメータを含むモデルクラス（太い黒の等高線）内の引き寄せの盆地に対応していると考えることができる。 計算結果は、課題がモデルのパラメータ設定に強い制約を与えることを示す。 すなわち、与えられた課題の最適化パラメータのセットは、元の空間に比べて非常に小さいということである。 これらの目標駆動モデルは、与えられた課題領域での行動の根底にあると考えられている脳領域のニューロンの応答特性をどの程度予測できるかについて評価することができる。 例えば、単語認識のために最適化されたモデルのユニット、聴覚皮質の一次領域、ベルト領域、パラベルト領域の応答特性と比較することができる。 また、モデルを互いに比較して、異なるタイプの課題がどの程度の神経構造の共有につながるかを判断することもできる。 また、様々な構成要素のルール（教師あり、教師なし、半教師あり）を研究して、それらが生後の発達や専門知識学習の間にどのように異なるダイナミクスにつながるかを判断することもできる（緑の破線のパス）。


3. 畳込みニューラルネット(CNN)

深層学習 (ディープラーニング) の中で 畳み込みニューラルネットワーク CNN と呼ばれるニューラルネットワークについて解説します。

最初に画像処理の概略を述べる CNN が，それまで主流であった従来の手法の性能を凌駕したことはすでに述べました。 CNN の特徴の一つに エンドツーエンド と呼ばれる考え方があります。 エンドツーエンドとは，従来手法によるパターン認識システムでは，専門家による手の込んだ詳細な作り込みを必要としていたことと異なり，面倒な作り込みをせずとも性能が向上したことを指します。

エンドツーエンドなニューラルネットワークにより，次のことが実現しました。

  • ニューラルネットワークの層ごとに，特徴抽出が行われ，抽出された特徴がより高次の層へと伝達される
  • ニューラルネットワークの各層では，比較的単純な特徴から次第に複雑な特徴へと段階的に変化する
  • 高次層にみられる特徴は低次層の特徴より大域的，普遍的である
  • 高次層のニューロンは，低次層で抽出された特徴を共有している

このことを簡単に説明してみます。

我々人間は，外界を認識するために必要な計算を，生物種としての発生の過程と，個人の発達を通しての経験に基づく認識システムを保持していると見ることができます。 従って我々の視覚認識には化石時代に始まる光の受容器としての眼の進化の歴史と発達を通じた個人の視覚経験が反映された結果でもあります。 人工知能の目標は，この複雑な特徴検出過程をどうやったらコンピュータが獲得できるかということでもあります。 外界を認識するために今日まで考案されてきたモデル（例えば，ニューラルネットワークサポートベクターマシンなどは）は複雑です。 ですがモデルを訓練するための学習方法はそれほど難しくありません。 この意味で画像認識課題が正しく動作するためのポイントは，認識システムが問題を解く事が可能なほど複雑であるかどうかではなく，十分に複雑が視覚環境，すなわち画像認識の場合，外部の艦橋を反映するために十分な量の像データを容易すことができるか否かにあります。 今日の CNN による画像認識性能の向上は，簡単な計算方法を用いて複雑な外部環境に適応できる認識システムを構築する方法が確立したからであると言うことが可能です。

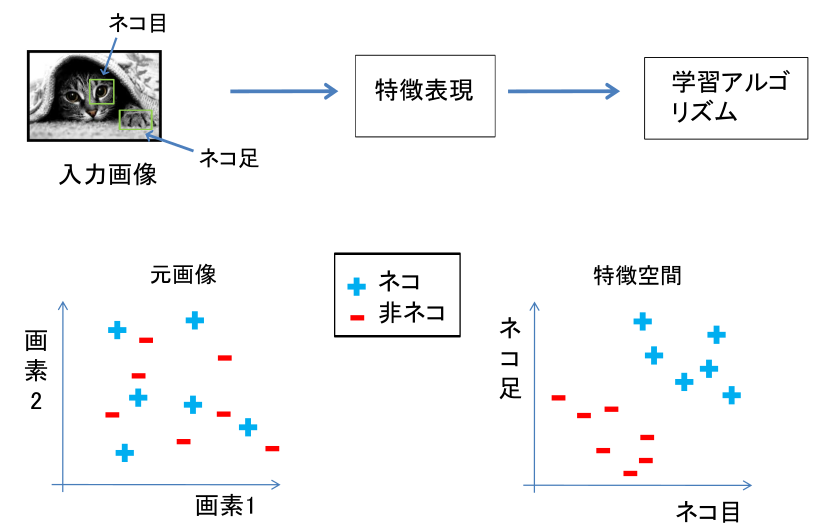
下図 に画像処理の例を挙げました。


Goodfellow et al. (2017) Fig.1 を改変

我々は 画像をほぼ瞬時に判断できます。 ですが画像認識の難しさは，入力画像が上図 に示されているように入力信号の数字の集まりでしか無いことです。 このようなデータを何度も経験することでネコを識別できるようにする必要があります。 コンピュータに入力される画像は数字の塊に過ぎません。

状況ごとにとるべき操作を命令として逐一コンピュータに与える指示する手順の集まりのことをコンピュータプログラムと呼びます。人間がコンピュータに与えることができる操作や命令によって画像認識システムを作る場合，命令そのものが膨大になったり，そもそも説明することが難しかったりします。 例を挙げれば，お母さんを思い浮かべてくださいと言われれば誰でも，それぞれ異なるイメージであれ思い浮かべることができます。また，提示された画像が自分の母親のものであるか，別の女性であるかの判断は人間であれば簡単です。ところがコンピュータには難しい課題となります。 加えて母親の特徴をコンピュータに理解できる命令としてプログラムすることも難しい課題です。つまり自分の母親の特徴を曖昧な言葉でなく明確に説明するとなるととても難しい課題となります。 というのは，女性の顔写真であればどの写真も似ていると言えるからです。顔の造形や輪郭，髪の位置などはどの画像も類似していることでしょう。ところがコンピュータにはこの似ている，似ていいないの区別が難しいのです。

加えて，同一ネコの画像であっても，被写体の向き視線の方向や光源の位置や撮影条件が異なれば画像としては異なります。 下図に示したように入力画像の中の特定の値だけを調べてみても，入力画像がネコであ る，そうではないかを判断することは難しい課題になります。

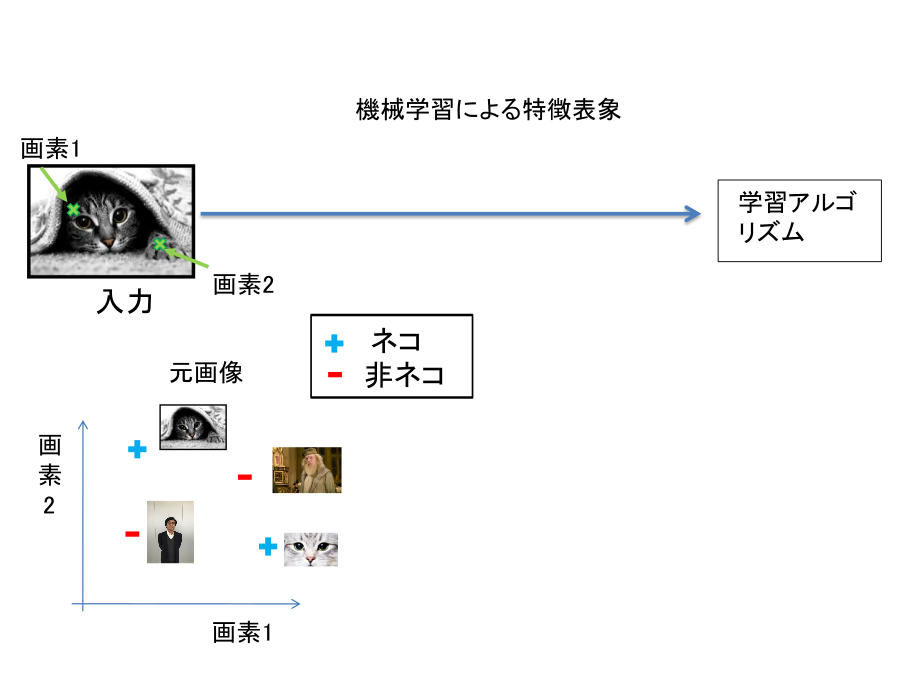
現在の画像認識では，特定の画素の情報に依存せずに，入力画像が持っている特徴 をとらえるように設計されます。たとえば，ネコを認識するために必要ことは，ネ コに特徴的な「ネコ目」や「ネコ足」を検出することであると考えます。入力画像 から，ネコの持つ特徴を抽出することができれば，それらの特徴を持っている入力 画像はネコであると判断して良いことになります(下図 )。

下図 は，音声認識と画像認識の両分野において CNN が用いられる以前の従来手法 をまとめたものです。

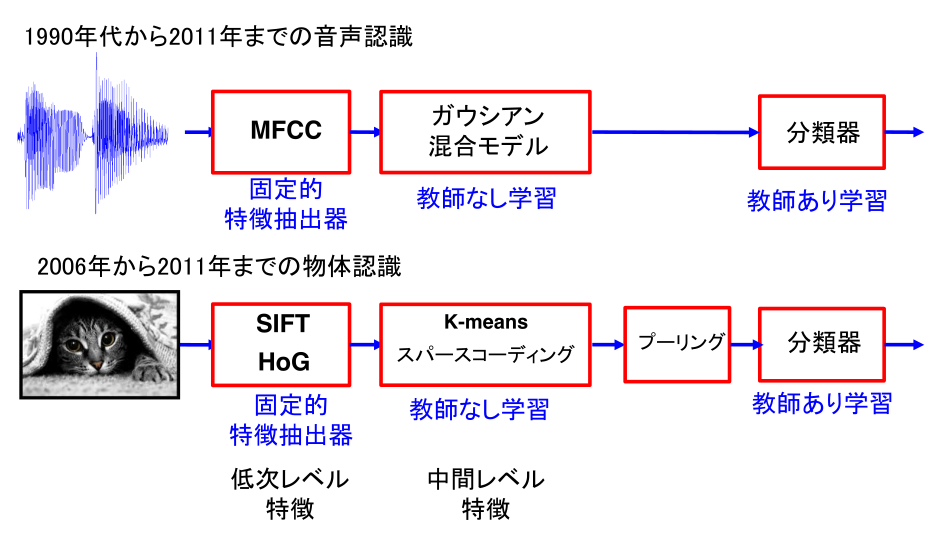
上図 のような従来手法に対して，CNN ではエンドツーエンドな特徴抽出を多層多段に重ねることによって複雑な特徴を抽出(検出)しようとしています (下図)。

コンピュータにはネコ目特徴検出器，ネコ足特徴検出器は備わっていません。そこで画像認識研究では，画像の統計的性質に基づいて特徴検出器を算出する方法を探す努力が行われてきました。 しかし，コンピュータにネコ目特徴やネコ足特徴を教えるは容易なことではありません。 このことは画像処理の分野だけに限りません，音声認識でも言語情報処理でもそれぞれの特徴器を一つ一つ定義し，チューニングするのは時間がかかり，専門的な知識も必要で困難な作業でした。

領域切り出し

画像処理と言語処理との融合


まとめると，1950 年代後半以来:固定的，手工芸的特徴抽出器と学習可能な分類器を用いた認識システムを作ることが試みられてきたといえます。 これに対して CNN が主流となった現在はエンドツーエンドで学習可能な特徴抽出器を多数重ね合わせることで性能が向上しました。

夢のような話が続きましたが，本節の最後に逆に CNN は簡単に騙すことができる例 を挙げておきます。

図では，左の画像が入力画像で，CNN は確信度 57.7パーセントでパンダである認識しました。 ところがこの画像に 0.007だけ意味のない画像(図中央)を加えるた画像(図右)を CNN は 99.3パーセントの確信度でテナガザル (gibbon)と判断しました。この例はここでは詳しく触れることはしませんが 敵対的学習と呼ぶ訓練手法を説明する際に用いられた例です 。

この例からも分かることは以下のようにまとめられるでしょう。 すなわち，人間の脳を模したニューラルネットワークである CNN が大規模化像認識チャレンジにおいて人間の認識性能を越えたと報道されました。 ですが，人間の視覚認識を完全に実現したと考えるのは早計で，解くべき課題は未だ多数あるということです。 この状況は，音声認識や言語情報処理でも同様であると言えます。

認知計算論的神経科学 Cognitive computational neuroscience


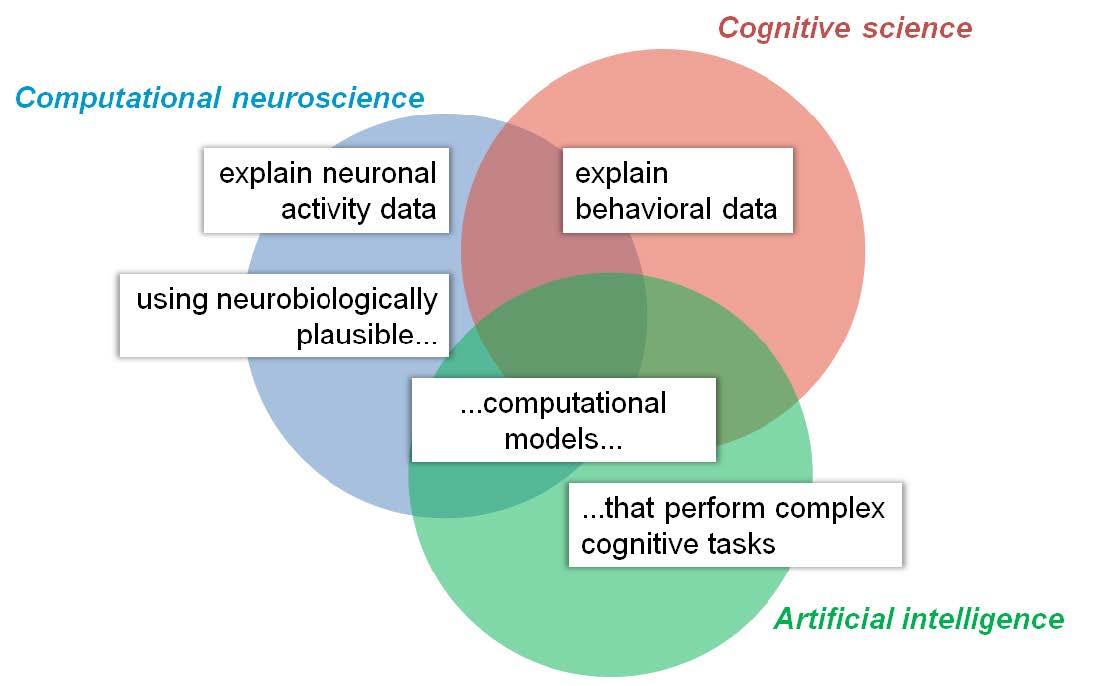
Kriegeskorte and Doglas (2018) Fig. 2より

脳の機能を理解することはどういうことか？ 認知計算神経科学の目的は実世界の認知課題を遂行可能で，生物学的妥当性を持つ計算モデルを用いて動物や人間の神経活動と行動の多くの観測結果を説明することである。 歴史的には各分野（円）はこれら課題の回問題（白ラベル）に取り組んできた。

CNN の詳細

通常のニューラルネットワークでは，直下層のニューロンとそのすぐ上の層の全ニューロンと結合を有する。一方 CNN ではその結合が部分的である。 各ニューロンは多入力一出力の信号変換機とみなすことができ，活性化関数に非線形な関数を用いる点は通常のニューラルネットワークと同様。

画像処理を考える場合，典型的には一枚の入力静止画画像は 3 次元データである。次元は幅w，高さh，奥行きd であり，入力画像では奥行きが３次元，すなわち赤緑青の三原色。出力ニューロンへの入力は局所結合から小領域に限局される。

1. CNNの構成

CNN は以下のいずれかの層から構成される：

  1. 畳込み層
  2. プーリング層
  3. 完全結合層（通常のニューラルネットワークと正確に同じもの，CNN では最終 1 層または最終 1,2 層に用いる）

入力信号はパラメータの値が異なる活性化関数によって非線形変換される。 畳込み層とプーリング層と複数積み重ねることで多層化を実現し，深層ニューラルネットワークとなる。

例：

  • 画像データを出力信号へ変換
  • 各層は別々の役割（畳込み，全結合，ReLU, プーリング）
  • 入力信号は 3 次元データ，出力信号も 3 次元データ
  • 学習すべきパラメータを持つ層は畳込み層，全結合層
  • 学習すべきパラメータを持たない層は ReLU 層とプーリング層
  • ハイパーパラメータを持つ層は畳込み層, 全結合層, プーリング層
  • ハイパーパラメータを持たない層は ReLU層

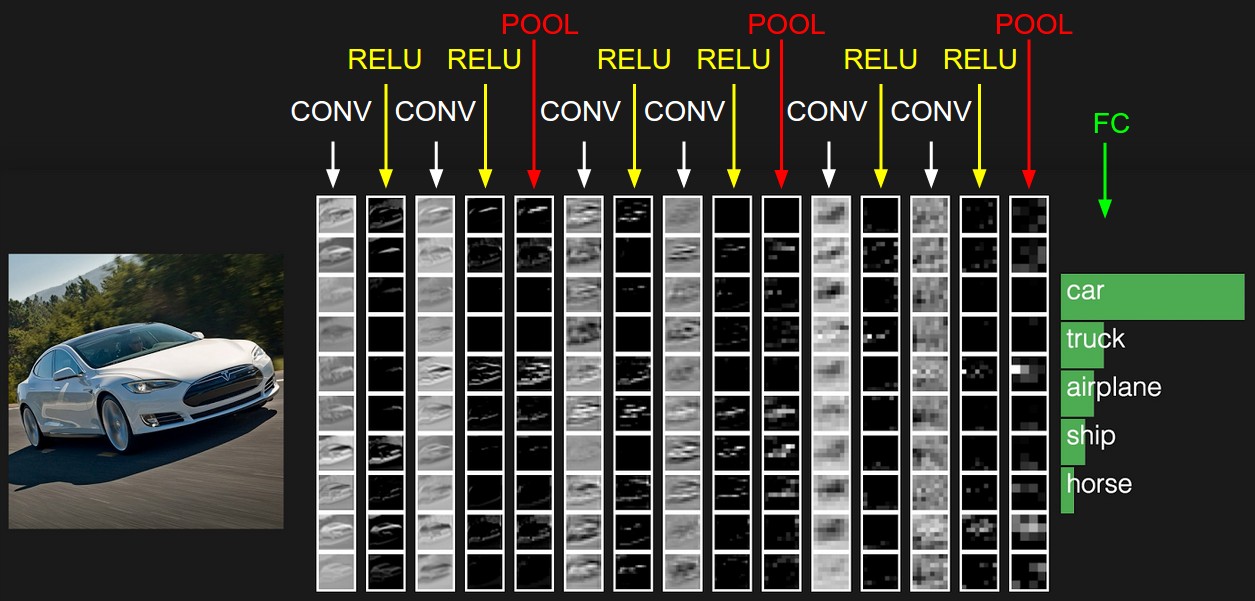
CNN アーキテクチャ: 入力層は生画像の画素値(左)を格納、最後層は分類確率(右)を出力。処理経路に沿った活性の各ボリュームは列として示されている。3Dボリュームを視覚化することは難しいため、各ボリュームのスライスを行ごとに配置してある。最終層のボリュームは各クラスのスコアを保持するが、ソートされた上位5スコアだけを視覚化し、それぞれのラベルを印刷してある。

  • 入力層[32x32x3]: 信号は画像の生データ（画素値）幅w(32)，高さh(32)、色チャネル3(R, G, B)
  • 畳込み層: 下位層の限局された小領域のニューロンの出力の荷重付き総和を計算(内積，ドット積）。12個のフィルタを使用すると[32x32x12]となる。
  • ReLU層の活性化関数は ReLU (Recutified Linear Unit)
  • プーリング層: 空間次元（幅,高さ）に沿ってダウンサンプリングを実行。[16x16x12]のようになる。
  • 全結合層はクラスに属する確率を計算: 10 の数字のそれぞれが CIFAR-10 の 10 カテゴリーの分類確率に対応するサイズ[1x1x10]に変換。通常のニューラルネットワーク同様、全結合層のニューロンは前層の全ニューロンと結合する。

CNN は元画像（入力層）から分類確率（出力層）へ変換。学習すべきパラメータを持つ層（畳込み層，全結合層）とパラメータを持たない層（ReLU層）が存在。畳込み層と全結合層のパラメータは勾配降下法で訓練

2. 畳込層


ネオコグニトロンの概略図(Fukushima, 1979)


LeNet5 (LeCun, 1998)


アレックスネット(Krizensky et al. 2012)
アレックスネットの出力例(Krizensky et al. 2012)

  • 畳込み層のパラメータは学習可能なフィルタの組
  • 全フィルタは空間的に（幅と高さに沿って）小さくなる
  • フィルタは入力信号の深さと同一
  • 第1層のフィルタサイズは例えば 5×5×3（5 画素分の幅，高さ，と深さ 3（３原色の色チャンネル）
  • 各層の順方向の計算は入力信号の幅と高さに沿って各フィルタを水平または垂直方向へスライド
  • フィルタの各値と入力信号の特定の位置の信号との内積（ドット積）。
  • 入力信号に沿って水平，垂直方向にフィルタをスライド
  • 各空間位置でフィルタの応答を定める 2 次元の活性化地図が生成される
  • 学習の結果獲得されるフィルタの形状には、方位検出器，色ブロッブ，生理学的には視覚野のニューロンの応答特性に類似
  • 上位層のフィルタには複雑な視覚パタンに対応する表象が獲得される
  • 各畳込み層全体では学習すべき入力信号をすべて網羅するフィルタの集合が形成される
  • 各フィルタは相異なる 2 次元の活性化地図を形成
  • 各フィルタの応答特性とみなすことが可能な活性化地図
  • フィルタの奥行き次元に沿って荷重総和を計算し、出力信号を生成

局所結合: 画像のような高次元の入力を処理する場合，下位層の全ニューロンと上位層の全ニューロンとを接続することは 責任割当問題回避 の観点からもパラメータ数の増加は現実的ではない。
代わりに各ニューロンを入力ボリュームのローカル領域のみに接続。空間的領域はニューロンの 受容野 と呼ばれるハイパーパラメータ（フィルタサイズとも言う）。深さ次元に沿った接続性＝入力層の深さ次元。 空間次元（幅と高さ）と深さ次元をどのように扱うかにより，この非対称性を再び強調することが重要です。ニューロン間の結合は空間次元（幅と高さ）にそって限局的。入力次元の深さ全体を常にカバーする。

  • 例1: 入力層のサイズが[32x32x3]（RGB CIFAR-10画像データセットなど）であれば受容野（フィルタサイズ）が 5x5 とすれば，畳込み層内の各ニューロンは入力層の [5x5x3] 小領域への結合係数を持つ。各小領域毎に 5x5x3=75 の重み係数と 1 つのバイアス項が必要である。深さ次元に沿った上層のニューロンから下位層のニューロンへの結合は下位層の深さ(色チャンネル数)と等しく 3 である。

  • 例2: 入力ボリュームのサイズが[16x16x20]であるとすると 3x3 の受容野サイズで畳込層の全ニューロンの合計は 3x3x20=180 接続。接続性は空間的に局在する（3x3）が，入力深度（20）に沿っては完全結合

空間配置: 出力層ニューロンの数と配置については 3 つのハイパーパラメータで出力ニューロン数が定まる。

  1. 深さ数(フィルタ数)
  2. ストライド幅

  3. ゼロパディング

  4. 1 出力層ニューロン数のことを出力層の 深さ 数と呼ぶハイパーパラメータである。深さ数とはフィルタ数（カーネル数）とも呼ばれる。第 1 畳込み層が生画像であれば，奥行き次元を構成する各ニューロンによって種々の方位を持つ線分(エッジ検出細胞)や色ブロッブのような特徴表現を獲得可能となる。入力の同じ領域を 深さ列 とするニューロン集団を ファイバ ともいう。

  5. 2 フィルタを上下左右にずらす幅を ストライド幅 と呼ぶ。ストライド幅が 1 ならフィルタを 1 画素ずつ移動することを意味する。ストライドが 2ならフィルタは一度に 2 画素ずつジャンプさせる。ストライド幅が大きければ入力信号のサンプリング間隔が大きく広がることを意味する。ストライド幅が大きくなれば上位層のニューロン数は減少する。

  6. 3 入力の境界上の値をゼロで埋め込むことがある。これを ゼロパディング という。ゼロパディングの量はハイパーパラメータである。ゼロパディングにより出力層ニューロンの数を制御できる。下位層の空間情報を正確に保存するには入力と出力の幅，高さは同じである必要がある。

入力層のニューロン数を ，上位にある畳込み層のニューロン数を ，とすれば出力層に必要なニューロン数 は，周辺のゼロパディング を とすれば で算出できる。 たとえば下図でストライド とゼロパディング であれば入力 でフィルタサイズが であれば 5x5(=S=(7-3+2x0)/1+1=5) の出力である。 ストライド ならば となる。


空間配置の例：入力空間の次元（x軸）が1つで受容野サイズ F=3 の場合，入力サイズ W=5, ゼロパディング P=1 であれば，
左図：出力層ニューロン数は (5-3+2)/1+1=5 の出力層ニューロン数となる。ストライド数 S=1 の場合。
右図：s=2，出力層ニューロン数 (5-3+2)/2+1=3 となる。ストライド S=3 ならばボリューム全体にきちんと収まらない場合もでてくる。数式で表現すれば $(5-3+2)=4$ は 3 で割り切れないので、整数の値として一意に決定はできない。
ニューロン結合係数は（右端に示されている）[1,0,-1]でありバイアスはゼロ。この重みはすべての黄色ニューロンで共有される。

ゼロパディング: 上例では入力次元が 5，出力次元が 5 であった。 これは受容野が 3 でゼロ埋め込みを1としたためである。ゼロ埋め込みが使用されていない場合、出力ボリュームは、どれだけの数のニューロンが元の入力に「フィット」するのであろうかという理由で、空間次元がわずか 3 であったであろう。 ストライドが のとき、ゼロ埋め込みを に設定すると、入力ボリュームと出力ボリュームが空間的に同じサイズになる。 このようにゼロパディングを使用することは一般的である。CNNについて詳しく説明している完全な理由について説明する。

ストライドの制約: 空間配置ハイパーパラメータには相互の制約があることに注意。たとえば入力に というサイズがあり、ゼロパディングは ではなく、フィルタサイズは, よりストライド を使用することは不可能である。 すなわち整数ではなくニューロンが入力にわたってきれいにかつ対称的に "適合" しないことを示す。

AlexNet の論文では，第一畳込層は受容野サイズ ，ストライド，ゼロパディングなし。
畳込層 の深さ 。畳込層の出力サイズは [55x55x96]。55x55x96 ニューロンは入力領域 [11x11x3] と連結。全深度列 96 個のニューロンは同じ入力領域[11×11×3]に繋がる。論文中には(224-11)/4+1 となっている。パディングについての記載はない。

パラメータ共有 パラメータ数を制御するために畳み込み層で使用される。上記の実世界の例を使用すると、最初の畳故意層には 55x55x96=290,400のニューロンがあり、それぞれ 11x11x3=363 の重みと1のバイアスがある。これにより CNN 単独の第 1 層に最大 290400x364=105,705,600 のパラメータが追加される。

パラメータ共有 により学習すべきパラメータ数が減少する。 例えば [55x55x96] のフィルタでは深さ次元は 96 個のニューロンで，各深さで同じ結合係数を使うことにすれば ユニークな結合係数は計 96x11x11x3=34,848 となるので総パラメータ数は 34,944 となる(バイアス項 +96)。各深さで全ニューロン(55x55)は同じパラメータを使用する。逆伝播での学習では，全ニューロンの全結合係数の勾配を計算する必要がある。各勾配は各深さごとに加算され 1 つの深さあたり一つの結合係数集合を用いる。

ある深さの全ニューロンが同じ重み係数ベクトルを共有する場合，畳込み層の順方向パスは各深さスライス内で入力ボリュームとのニューロンの重みの 畳み込み として計算できることに注意。結合荷重係数集合のことを フィルタ または カーネル と呼ぶ。入力信号との間で畳込み演算を行うこととなる。


AlexNet の学習済フィルタ例: 図の 96 個のフィルタは サイズ [11x11x3]。 それぞれが 1 つの深さ内の $55\times55$ ニューロンで共有されている。 画像の任意の位置で水平エッジ検出が必要な場合，画像の並進不変構造 translationall-invariant structure 仮定により画像中の他の場所でも有効である。 畳込み層の出力ニューロン数は $55\times55$ 個の異なる位置すべてで水平エッジの検出を再学習する必要はない。

3. プーリング層

CNN では，連続する畳込み層間にプーリング層を挿入するのが一般的。プーリング層の役割は，空間次元の大きさに減少させることである。パラメータ，すなわち計算量を減らし，過学習を制御できる。プーリング層は入力の各深さ毎に独立して動作する。最大値のみをとり他の値を捨てることを マックスプーリング と呼ぶ。サイズが 2x2 のフィルタによるプーリング層では，入力の深さごとに つのダウンサンプルを適用し、幅と高さに沿って2ずつ増やして75％の情報を破棄する。この場合 4 つの数値のうち最大値を採用することになる。


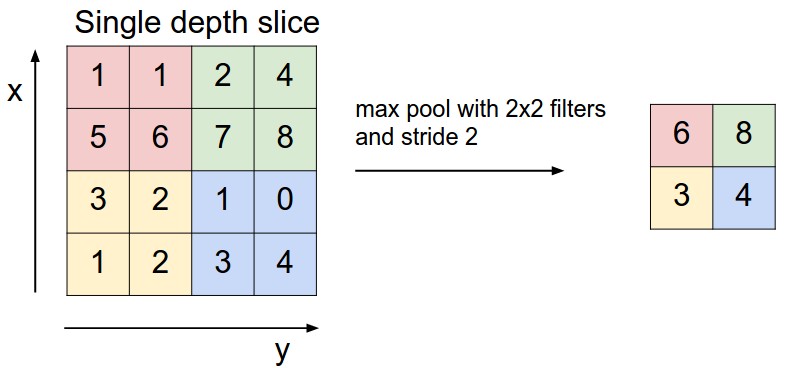
一般的なダウンサンプリング演算は マックスプーリング である。図では ストライド 2 すなわち 4 つの数値の中の最大値

平均プーリング. マックスプーリングではなく L2正則化プーリング を行う場合もある。平均プーリングは歴史的な意味あいがあるがマックスプーリングの方が性能が良いとの報告がある。ある画像位置には物理的に一つの値だけが存在するという視覚情報処理が仮定すべき外界の物理的制約を反映していると文学的に解釈することも可能である。


プーリング層では，入力層ニューロン数の各深さについて空間的ダウンサンプリングを行う。この例は サイズ[224x224x64]の入力層ニューロン数がフィルタサイズ 2 でプールされ，サイズ 2 の出力ニューロン数 [112x112x64] は 2 倍である。奥行き数が保持されている。

4. 全結合層

全結合層のニューロンは、通常のニューラルネットワークと同じ
前層の全ニューロンと結合を持つ

5. CNN アーキテクチャ

  1. 畳込層
  2. プーリング層
  3. 全結合層

層は以上 3 種類が一般的。

6. CNN の層構造

入力層 [[畳込層 ReLU] プーリング(?)] M [全結合層 ReLU] K 全結合層

最近のトレンドとしては大きなフィルタより小さなフィルタが好まれる傾向にある。
[3x3] が好まれる理由はど真ん中がある奇関数を暗黙に仮定しているためだと思われる（浅川の妄想）。 その代わり多段にすれば [3x3] が２層で ［5x5]，３層で[7x7]の受容野を形成できるから受容野の広さを層の深さとして実装しているとも解釈できる。１層で[7x7]の受容野より３層で[7x7]の受容野を実現した方が the simpler, the better の原則に沿っているとも（文学的）解釈が可能である（またしても浅川妄想）。

バックプロパゲーションの計算時に広い受容野を作るより層を分けた方が GPU のメモリに乗せやすいと言う計算上の利点もある。


Lillicrap et al. (2020) Fig. 7 を改変