ディープラーニングの心理学的解釈 (心理学特講IIIA)¶
第 11 回 精神医学(統合失調症, 強迫神経症, 依存症, 幻覚幻聴)
## 実習
参考文献¶
- 感情とはそもそも何なのか,乾 敏郎, ミネルヴァ書房,2018
- 計算論的精神医学, 国里,片平,沖村,山下, 勁草書房, 2019
資料¶
(自由エネルギーの最小化) = (予測誤差を最小化するように信念を書き換え予測を最適化)+(予測誤差)を最小化するような行動をとる)
(自由エネルギー) = (内部エネルギー)-(エントロピー)
乾(2018, p. 134)
ニューラルネットワークの物理学メタファー¶
- 2019年度駒澤大学文学部開講科目,心理学特講 IIIA は,文化,思想,に関する議論をする科目ではありません。 ましてや,文壇,言論界,などに対するいかなるメッセージも含むものではありません。
- 駄菓子菓子,以下の出来事については考慮する必要があると考えます: ソーカル事件, and 知の欺瞞
- ただ 騙されない ようにしたいと願うだけです。
上記に対する精一杯の言い訳¶
- 我々の脳は数多の神経細胞から成り立っている。従って,我々の思想,行動,考え方,信念,抽象的思考,などはニューロンの働きに礎を置くと考えることができる。
- 一方,ブラーエ,ケプラー,ガリレイ,ニュートンと続く古典物理学の譜系と,物質が分子,原子,素粒子でなりたっているという
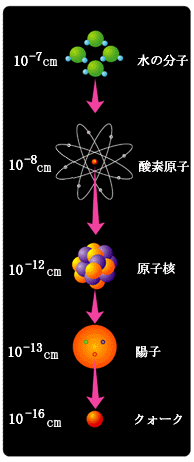
キッズサイエンティストより https://www2.kek.jp/kids/class/particle/class01-02.html
- たとえば,ダイエットをして 5Kg 減量に成功したという友人 A が,5g 痩せたというと頭おかしいと思うでしょう。鼻をかんだら 5g くらい減るでしょう。
- 同じように,健康のために毎日 5Km 走っているという友人 B が毎日 5Mm=5000Km (5 * 10^3)m 走っていると言い始めたら頭おかしいと思うでしょう。
- 単位が 異なると別次元の話と考えないと頭おかしいのです。東京からインドのコルカタまでの距離がおよそ 5167Km ほどだそうです
統計物理学,簡単にいえば単に統計の目的は,巨視的な物体,すなわち膨大な数の個別的な粒子 --- 原子や分子 --- からなる物体のぶるまいや性質を支配している特 別な型の法則を研究することである
ランダウ,リプシッツ,(1957) 統計物理学
上記のような統計物理学,熱力学で議論されてきたようなミクロな系(粒子の法則)とマクロな系(物体のふるまい)のアナロジーが,神経細胞と知的活動との間でも成り立 つのではないかという淡い期待。
計算論的精神医学: 幻の器官としての脳 (Friston, 2014)¶
- 脳機能の理論的枠組みによる定式化: 主観的信念や行動を,形式的な計算論的枠組み,すなわち神経生理学に基づくシナプス機構のレベルで捉える
- アクティブ(ベイジアン)推論と予測コーディング
- 自閉症の偏った心や統合失調症の円滑追跡眼球運動異常
予測符号化を支える階層的ニューロン間のメッセージ送受信システム
神経細胞の活動は、感覚入力の原因についての期待をコード化している。 この神経活動における期待は予測誤差を最小化しようとする。 この最小化は,皮質階層の異なるレベル間でのニューロンの再帰的な相互作用に依存している。 このモデルでは,表層の錐体細胞(赤い三角形)が,より高いレベルの深層の錐体細胞(黒い三角形)からのトップダウン予測と, 各レベルでの予測を比較していることが示されている。
強制マッチング錯視の予測符号化モデル
フリストンの言う自由エネルギーとは,ヘルムホルツの自由エネルギーを脳神経系に当てはめた仮説。
力学的エネルギー = 運動エネルギー + 位置エネルギー(ポテンシャル)
ヘルムホルツの自由エネルギー:
はヘルムホルツの自由エネルギー, は温度, はエントロピー。
- 熱力学の第一法則 エネルギー保存則
- 熱力学の第二法則
ギブスの自由エネルギー
フリストンを理解するための用語集 (Fristion, 2009) より¶
- カルバック-ライブラー (Kullback-Leibler) ダイバージェンス (divergence): 2 つの確率分布間の差の非可換的な尺度
- ベイジアンサプライズ:認識確率と事前確率の間のダイバージェンスに基づく顕在性の測度。認識できるデータ内の情報を計量している。
- 条件付き確率密度: または事後確率。あるデータが与えられた場合の,原因またはモデルパラメータの確率分布。観察されたデータから原因への確率的なマッピング
- 経験的事前確率: 階層モデルから導出される推定値。データに依存して認識確率への制約を与える
-
エントロピー: 確率の高いデータからサンプリングされた結果の平均的な驚き度合いを表す確率分布。エントロピーの低い密度とはが比較的予測可能であることを示している。
-
Ergodic: a process is ergodic if its long term time-average converges to its ensemble average. Ergodic processes that evolve for a long time forget their initial states.
-
エルゴード性: あるプロセスは,その長期的な時間平均がそのプロセスのアンサンブル平均に等しいことを表す。
- 自由エネルギー: 情報理論上の尺度。その下限は 生成モデルが与えられたとき,データをサンプリングした際の驚き度合い。
- 生成モデル:または順行モデルは原因から 観察された結果(データ)を推論する。生成モデルは通常,尤度 と事前確率が与えられた際に,データを得るためのパラメータによって記述される。
- 勾配降下法: 関数の最小値を求める最適化手法の一つ。 負の勾配に比例して引数を更新すること最適値を探索する手法。
- ヘルムホルツマシン: 生成モデルを使用して 認識密度を学習するモデル。データの潜在構造を学習する
-
事前確率: エンコードするデータの原因に関する確率分布。データを観察する前に,それらの原因についての信念。
-
Recognition density: or approximating conditional density is an approximate probability distribution of the causes of data. It is the product of inference or inverting a generative model.
-
認識確率: または近似条件つき確率。データの原因の近似的確率分布。推論または生成モデルの反転の産物
- 十分統計量: 確率密度をパラメータ化するのに十分な量
- サプライズ: または自己情報量。結果の負の対数確率。予測された結果があり得ない場合の量
フリストンの自由エネルギーとは¶
自由エネルギーとは,認識確率と感覚入力との関数である。 自由エネルギーは,認識確率の下で期待されるエネルギーとそのエントロピーの2つの項からなる。 エネルギーは,感覚入力 とその原因 の共起確率に関するサプライズである。 自由エネルギーは、感覚サンプルとその原因を生成する密度 と,その原因を認識する密度 の2つの密度に依存する。 この認識確率は,その十分な統計量である によって規定される。 これは脳によってコード化されていると仮定される。 このことは,自由エネルギーが,任意のシステムの生成モデル と,そのモデルの原因やパラメータの認識確率密度を誘導することを意味する。 これらの密度の関数形が与えられれば,自由エネルギーは感覚入力と十分な統計量の関数であるため,常に評価することが可能である。 自由エネルギーの原理は,変化することができるすべての量 (十分統計量 と行動 ) が,自由エネルギーを最小化することを主張している.